%pylab inline
colors = [[0.1,0.6,0.5], [0.9,0.2,0.5], [0.9,0.5,0.1]]

Populating the interactive namespace from numpy and matplotlib

Deconvolution in the frequency domain (DFT)

from PyDynamic.uncertainty.propagate_DFT import GUM_DFT,GUM_iDFT
from PyDynamic.uncertainty.propagate_DFT import DFT_deconv, AmpPhase2DFT
from PyDynamic.uncertainty.propagate_DFT import DFT_multiply

#%% reference data
ref_file = np.loadtxt("DFTdeconv reference_signal.dat")
time = ref_file[:,0]
ref_data = ref_file[:,1]
Ts = 2e-9
N = len(time)

#%% hydrophone calibration data
calib = np.loadtxt("DFTdeconv calibration.dat")
f = calib[:,0]
FR = calib[:,1]*np.exp(1j*calib[:,3])
Nf = 2*(len(f)-1)

uAmp = calib[:,2]
uPhas= calib[:,4]
UAP = np.r_[uAmp,uPhas*np.pi/180]**2

#%% measured hydrophone output signal
meas = np.loadtxt("DFTdeconv measured_signal.dat")
y = meas[:,1]
# assumed noise std
noise_std = 4e-4
Uy = noise_std**2

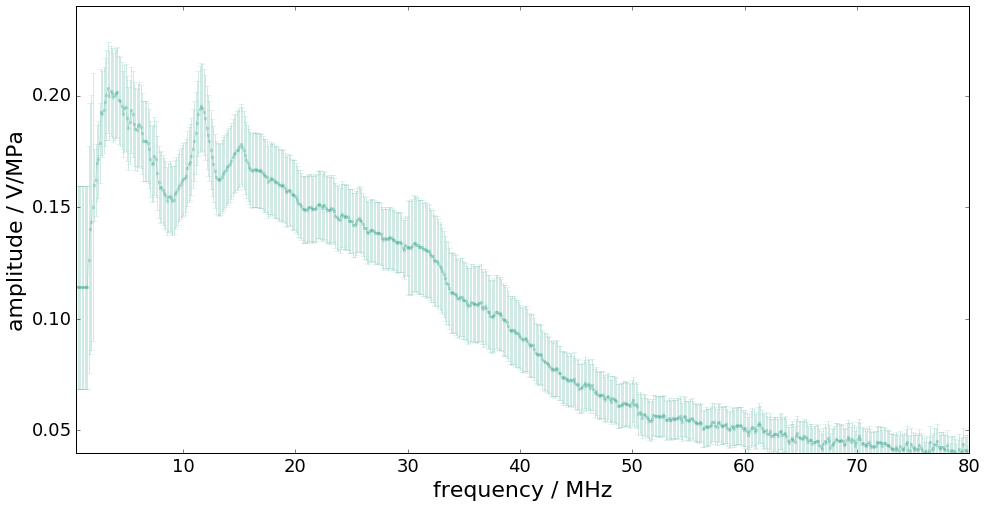
Consider knowledge about the measurement system is available in terms of its frequency response with uncertainties associated with amplitude and phase values.

\[\mathbf{H} = (\vert H(f_1) \vert, \ldots, \angle H(f_N))\]
\[u_H = (u_{\vert H(f_1) \vert}, \ldots, u_{\angle H(f_N)})\]
figure(figsize=(16,8))
errorbar(f * 1e-6, abs(FR), 2 * sqrt(UAP[:len(UAP) // 2]), fmt= ".-", alpha=0.2, color=colors[0])
xlim(0.5, 80)
ylim(0.04, 0.24)
xlabel("frequency / MHz", fontsize=22); tick_params(which= "both", labelsize=18)
ylabel("amplitude / V/MPa", fontsize=22);
_images/DFT_5_0.png 
figure(figsize=(16,8))
errorbar(f * 1e-6, unwrap(angle(FR)) * pi / 180, 2 * UAP[len(UAP) // 2:], fmt= ".-", alpha=0.2, color=colors[0])
xlim(0.5, 80)
ylim(-0.2, 0.3)
xlabel("frequency / MHz", fontsize=22); tick_params(which= "both", labelsize=18)
ylim(-1,1)
ylabel("phase / rad", fontsize=22);
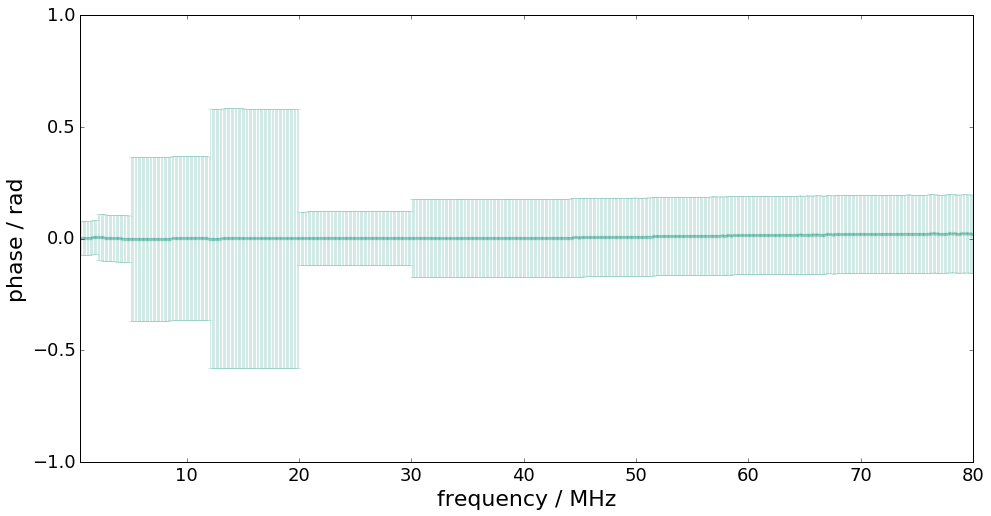
_images/DFT_6_0.png

The measurand is the input signal \(\mathbf{x}=(x_1,\ldots,x_M)\) to the measurement system with corresponding measurement model given by

\[y[n] = (h\ast x)[n] + \varepsilon[n]\]

Input estimation is here to be considered in the Fourier domain.

The estimation model equation is thus given by

\[\hat{x} = \mathcal{F}^{-1}\left( \frac{Y(f)}{H(f)}H_L(f) \right)\]

with - \(Y(f)\) the DFT of the measured system output signal - \(H_L(f)\) the frequency response of a low-pass filter

Estimation steps

  1. DFT of \(y\) and propagation of uncertainties to the frequency domain

  2. Propagation of uncertainties associated with amplitude and phase of system to corr. real and imaginary parts

  3. Division in the frequency domain and propagation of uncertainties

  4. Multiplication with low-pass filter and propagation of uncertainties

  5. Inverse DFT and propagation of uncertainties to the time domain

Propagation from time to frequency domain

With the DFT defined as

\[Y_k = \sum_{n=0}^{N-1} y_n \exp(-\mathrm{j} k\beta_n)\]

with \(\beta_n = 2\pi n /N\), the uncertainty associated with the DFT outcome represented in terms of real and imaginary parts, is given by

\[\begin{split}U_{Y} = \left( \begin{array}{cc} C_{\cos} U_y C_{\cos}^{\sf T} & C_{\cos} U_y C_{\sin}^{\sf T} \\ (C_{\cos} U_y C_{\sin}^{\sf T})^{\sf T} & C_{\sin} U_y C_{\sin}^{\sf T} \end{array}\right)\end{split}\]
Y,UY = GUM_DFT(y,Uy,N=Nf)

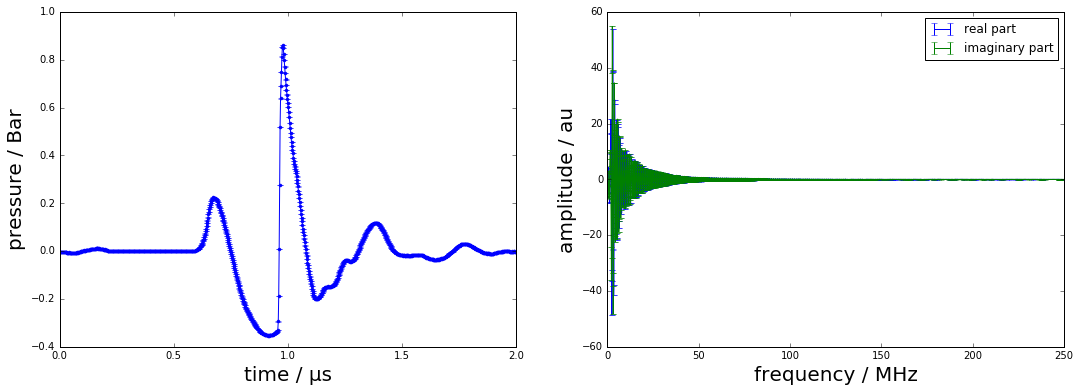
figure(figsize=(18,6))
subplot(121)
errorbar(time*1e6, y, sqrt(Uy)*ones_like(y),fmt=".-")
xlabel("time / µs",fontsize=20); ylabel("pressure / Bar",fontsize=20)
subplot(122)
errorbar(f*1e-6, Y[:len(f)],sqrt(UY[:len(f)]),label="real part")
errorbar(f*1e-6, Y[len(f):],sqrt(UY[len(f):]),label="imaginary part")
legend()
xlabel("frequency / MHz",fontsize=20); ylabel("amplitude / au",fontsize=20);
_images/DFT_13_0.png

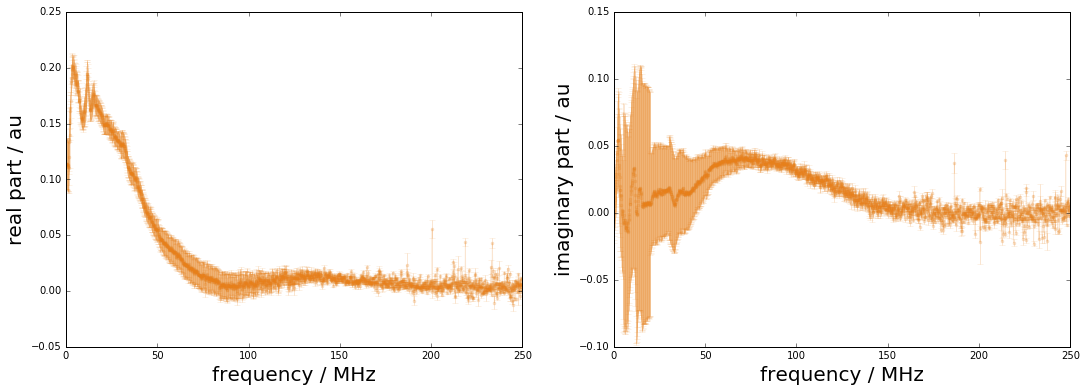
Uncertainties for measurement system w.r.t. real and imaginary parts

In practice, the frequency response of the measurement system is characterised in terms of its amplitude and phase values at a certain set of frequencies. GUM uncertainty evaluation, however, requires a representation by real and imaginary parts.

\[H_k = A_k \cos(P_k) + \mathrm{j} A_k\sin(P_k)\]

GUM uncertainty propagation

\[\begin{split}C_{RI} = \left( \begin{array}{cc} R_{A} & R_{P} \\ I_{A} & I_{P} \end{array}\right) .\end{split}\]
\[\begin{split}U_H = C_{RI} \left( \begin{array}{cc} U_{AA} & U_{AP} \\ U_{AP}^{\sf T} & U_{PP} \end{array} \right) C_{RI}^{\sf T} = \left( \begin{array}{cc} U_{11} & U_{12} \\ U_{21}^{\sf T} & U_{22} \end{array} \right) .\end{split}\]
H, UH = AmpPhase2DFT(np.abs(FR),np.angle(FR),UAP)

Nf = len(f)
figure(figsize=(18,6))
subplot(121)
errorbar(f*1e-6, H[:Nf], sqrt(diag(UH[:Nf,:Nf])),fmt=".-",color=colors[2],alpha=0.2)
xlabel("frequency / MHz",fontsize=20); ylabel("real part / au",fontsize=20)
subplot(122)
errorbar(f*1e-6, H[Nf:],sqrt(diag(UH[Nf:,Nf:])),fmt=".-",color=colors[2],alpha=0.2)
xlabel("frequency / MHz",fontsize=20); ylabel("imaginary part / au",fontsize=20);
_images/DFT_16_0.png

Deconvolution in the frequency domain

The deconvolution problem can be decomposed into a division by the system’s frequency response followed by a multiplication by a low-pass filter frequency response.

\[X(f) = \frac{Y(f)}{H(f)}H_L(f)\]

which in real and imaginary part becomes

\[X = \frac{(\Re_Y\Re_H + \Im_Y\Im_H)+\mathrm{j}(-\Re_Y\Im_H+\Im_Y\Re_H)}{\Re_H^2+\Im_H^2}(\Re_{H_L} + \mathrm{j}\Im_{H_L})\]

Sensitivities for division part

Uncertainty blocks for multiplication part

# low-pass filter for deconvolution
def lowpass(f,fcut=80e6):
    return 1/(1+1j*f/fcut)**2

HLc = lowpass(f)
HL = np.r_[np.real(HLc), np.imag(HLc)]

XH,UXH = DFT_deconv(H,Y,UH,UY)

XH, UXH = DFT_multiply(XH, UXH, HL)

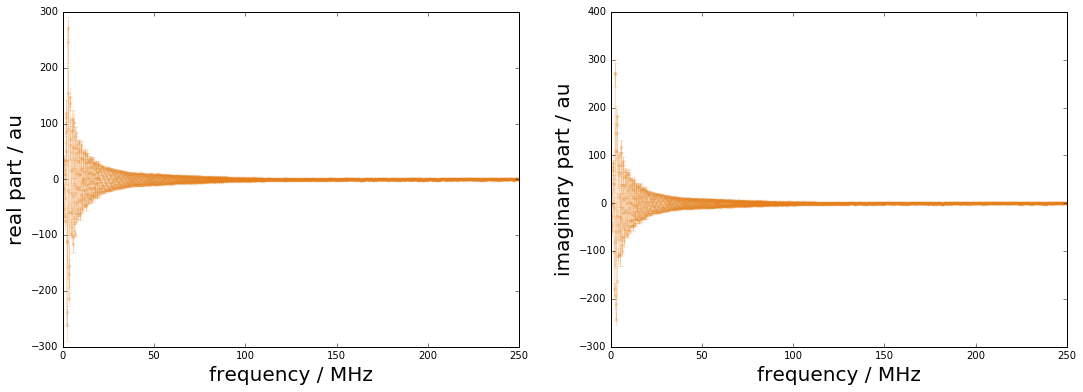
figure(figsize=(18,6))
subplot(121)
errorbar(f*1e-6, XH[:Nf], sqrt(diag(UXH[:Nf,:Nf])),fmt=".-",color=colors[2],alpha=0.2)
xlabel("frequency / MHz",fontsize=20); ylabel("real part / au",fontsize=20)
subplot(122)
errorbar(f*1e-6, XH[Nf:],sqrt(diag(UXH[Nf:,Nf:])),fmt=".-",color=colors[2],alpha=0.2)
xlabel("frequency / MHz",fontsize=20); ylabel("imaginary part / au",fontsize=20);
_images/DFT_22_0.png

Propagation from frequency to time domain

The inverse DFT equation is given by

\[X_n = \frac{1}{N} \sum_{k=0}^{N-1}(\Re_k\cos(k\beta_n)-\Im_k\sin(k\beta_n))\]

The sensitivities for the GUM propagation of uncertainties are then

GUM uncertainty propagation for the inverse DFT

xh,Uxh = GUM_iDFT(XH,UXH,Nx=N)

ux = np.sqrt(np.diag(Uxh))

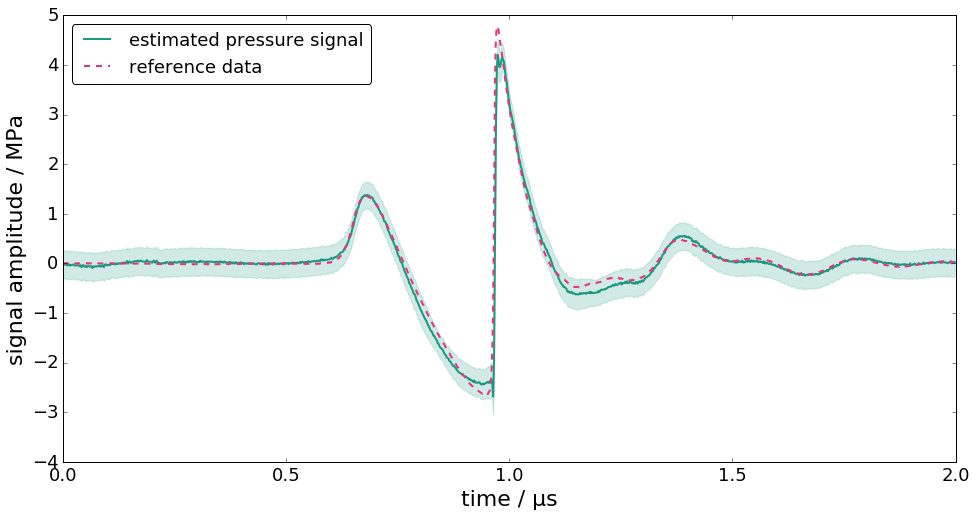
figure(figsize=(16,8))
plot(time*1e6,xh,label="estimated pressure signal",linewidth=2,color=colors[0])
plot(time * 1e6, ref_data, "--", label= "reference data", linewidth=2, color=colors[1])
fill_between(time * 1e6, xh + 2 * ux, xh - 2 * ux, alpha=0.2, color=colors[0])
xlabel("time / µs", fontsize=22)
ylabel("signal amplitude / MPa", fontsize=22)
tick_params(which= "major", labelsize=18)
legend(loc= "upper left", fontsize=18, fancybox=True)
xlim(0, 2);
_images/DFT_26_0.png 
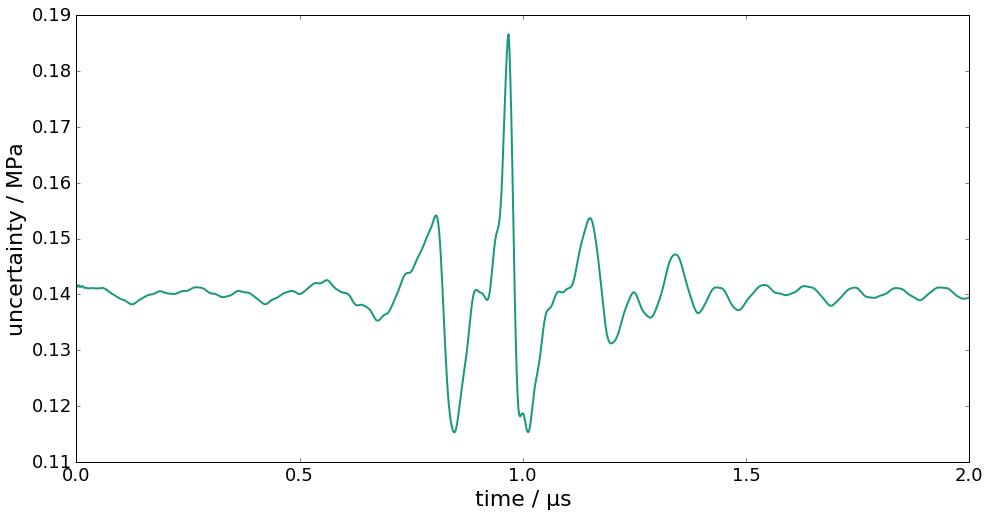
figure(figsize=(16,8))
plot(time * 1e6, ux, label= "uncertainty", linewidth=2, color=colors[0])
xlabel("time / µs", fontsize=22)
ylabel("uncertainty / MPa", fontsize=22)
tick_params(which= "major", labelsize=18)
xlim(0,2);
_images/DFT_27_0.png

Summary of PyDynamic workflow for deconvolution in DFT domain

Y,UY = GUM_DFT(y,Uy,N=Nf)

H, UH = AmpPhase2DFT(A, P, UAP)

XH,UXH = DFT_deconv(H,Y,UH,UY)

XH, UXH = DFT_multiply(XH, UXH, HL)