%pylab inline
pylab.rcParams['figure.figsize'] = (16.0, 8.0)
from PyDynamic import GUM_DFT

Populating the interactive namespace from numpy and matplotlib

DFT and inverse DFT with PyDynamic - best practice guide

The discrete Fourier transform (DFT) and its inverse (iDFT) are common tools in dynamic metrology. For the corresponding propagation of uncertainties, PyDynamic implements the main tools required:

Uncertainty propagation for the discrete Fourier transform

GUM_DFT(x,Ux,N=None,window=None,CxCos=None,CxSin=None,returnC=False,mask=None)

Uncertainty propagation for the inverse discrete Fourier transform

GUM_iDFT(F,UF,Nx=None,Cc=None,Cs=None,returnC=False)

Uncertainty propagation for convolution in the frequency domain

DFT_multiply(Y, UY, F, UF=None)

Uncertainty propagation for deconvolution in the frequency domain

DFT_deconv(H, Y, UH, UY)

In the following we discuss common use cases for these methods and present guidance on how to utilize the optional arguments of the above methods.

1) Discrete Fourier Transform (DFT)

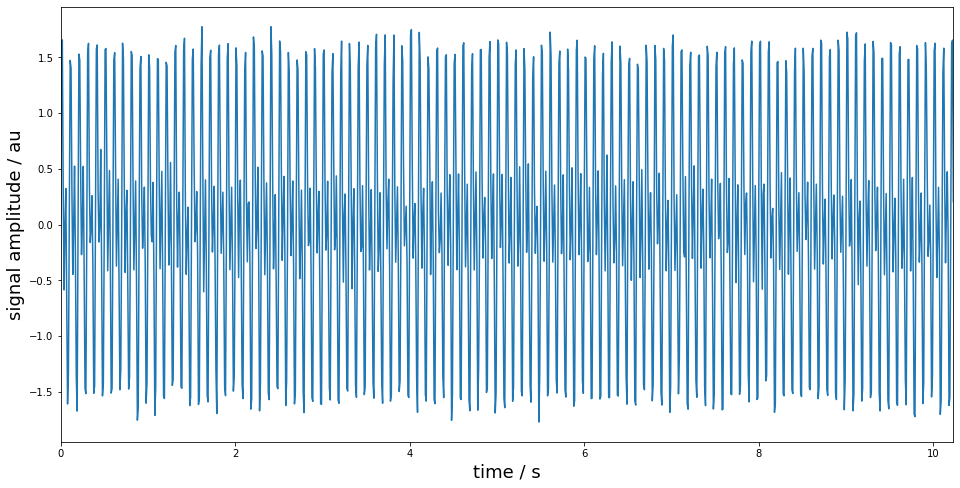
The first and most basic scenario is the application of the discrete Fourier transform to analyse a time domain signal in the frequency domain.

Fs = 100    # sampling frequency in Hz
Ts = 1/Fs   # sampling interval in s
N  = 1024   # number of samples
time = arange(0, N*Ts, Ts)  # time instants
noise_std = 0.1    # signal noise standard deviation
# time domain signal
x = sin(2*pi*Fs/10*time) + sin(2*pi*Fs/5*time) + random.randn(len(time))*noise_std

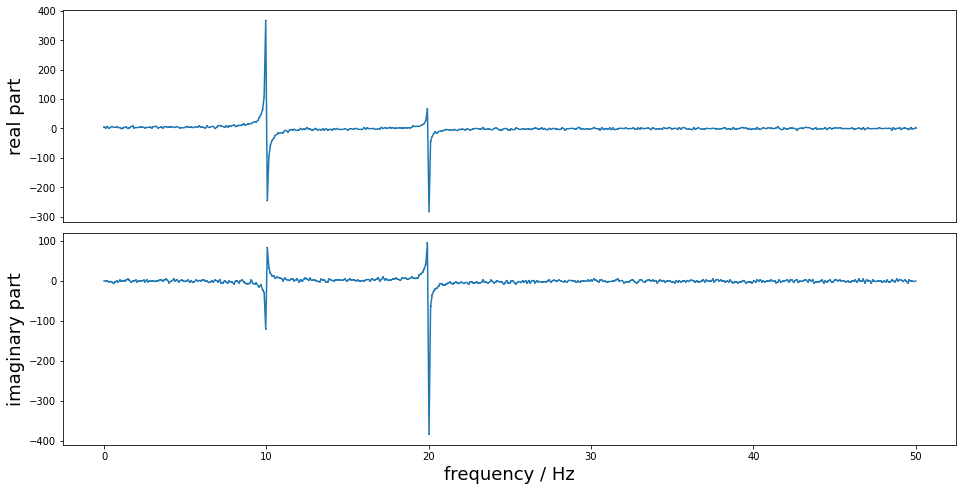
X, UX = GUM_DFT(x, noise_std**2)    # application of DFT with propagation of uncertainties
f = fft.rfftfreq(N, Ts)   # frequency values

figure()
plot(time, x)
xlim(time[0], time[-1])
xlabel("time / s", fontsize=18)
ylabel("signal amplitude / au", fontsize=18);

figure()
subplot(211)
errorbar(f, X[:len(f)], sqrt(UX[:len(f)]))
ylabel("real part", fontsize=18)
xticks([])
subplot(212)
errorbar(f, X[len(f):], sqrt(UX[len(f):]))
ylabel("imaginary part", fontsize=18)
xlabel("frequency / Hz", fontsize=18)
subplots_adjust(hspace=0.05)